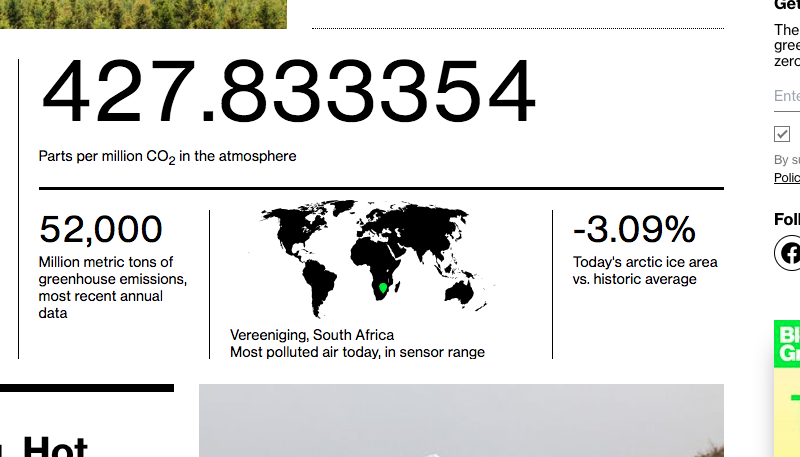
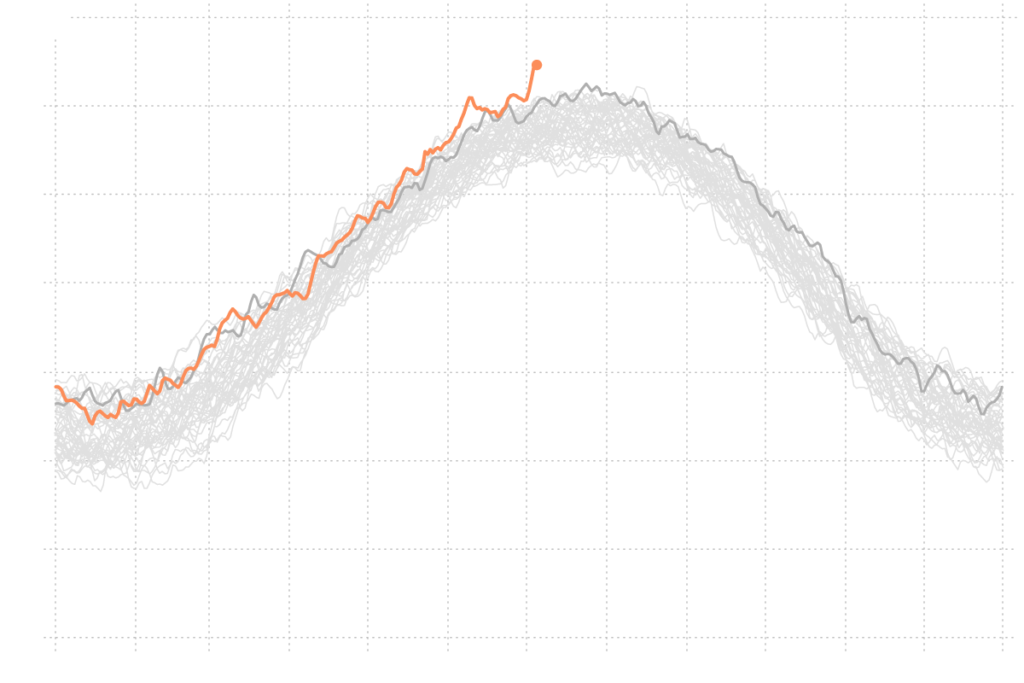
Weird convergence on how we distinguish work vs. labor that slices into entirely new territory when merged with sports gambling:
There is a way to make money, or at least not lose money, gambling on sports, and people who do it. That work involves crunching numbers, diversifying risk, seeking out small inefficiencies; it is, more or less, a job. A friend I spoke to for the story made a bunch of money betting the under on steals for various defense-deficient NBA guards. It’s not glamorous, it’s not juicy, it provides no mondo paydays. It’s barely fun at all. Again: it’s work.
Sports gambling apps do not want people to gamble like that. What they want bettors to do is put money on parlays. Apps push them in that direction constantly, even offering “no-risk parlays” to whet a prospective gambler’s appetite for the harder stuff. When I mentioned slot machine gambling to Dr. Fong, he immediately mentioned the same-game parlay. It’s an inevitable winner for casinos that also looks and feels good for the casual gambler.
In Addiction by Design, Schüll talks to slot machine designers about the process of making an effective slot machine. (They’re all from Australia, for some reason.) They tell her that it’s mostly a matter of feeling—finding a way to build in enough winning to maintain hope in the player, but also enough losing to make it profitable for the casino. It’s pretty nauseating; reading about otherwise sane people succumbing to sophisticated Skinner Boxes is dispiriting, and terrifying.
Here is one way that could all look: You watch a game with the app open. It gives you a personalized stream of quick, ever-changing, algorithmically generated bets. It also tracks what you will bet on and what you won’t, and then adjusts to create something akin to a personalized slot machine; the idea is to create an experience that feels good to you. If you are even a little bit inclined toward problem gambling, this will bury itself deep, and it will take your money; it will all be, as it currently is in 30 states, legal. And you can play like this until the government or a medical professional intervenes, or doesn’t. Everyone with any skin in the game—every business interest that sees its fans as a renewable resource—wants that to exist.
Turnip-truck green mixed with $$$-green produces no great good but a whole lot of parting.